3. The R Squared Value of a Fit#

3.1. Lesson overview#

It is important to quantify how “well” a fitted mathematical function matches a data set. One commonly used metric is called the “coefficient of determination” or the “R squared” value (often denoted as R²). In this lesson, we will show how to calculate R² when fitting data. Our focus will be on the practical implementation of R² using Python, and will skip on the theory behind the value. A good source on the basics of R² can be found here.

3.2. Topics taught / reviewed#

Calculating the R² of a fit.
Determining the mean of an array using the numpy.mean() function.
Finding the sum of an array using the numpy.sum() function.

3.3. Calculating R squared#

To demonstrate how to calculate R², let’s revisit our Ohm’s law fitting example from an earlier lesson. The compiled code block that loads the raw data, fits the data, plots both the raw data and fitted line, and prints out the fitting results to the shell is shown below:

# Load libraries
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import curve_fit

# Create function to fit
def linearFunc(x, intercept, slope):
    y = intercept + slope * x
    return y

# Load data and separate columns
data1 = np.loadtxt("./example_data/IV_data_no_uncertainty.csv", delimiter = ",", skiprows = 2)

current = data1[:, 0]
voltage = data1[:, 1]

# Perform the least-squares fitting
popt, pcov = curve_fit(linearFunc, current, voltage)

# Extract out the fitted parameters and standard errors
intercept = popt[0]
slope = popt[1]
intercept_err = np.sqrt(pcov[0][0])
slope_err = np.sqrt(pcov[1][1])

# Create figure
fig1 = plt.figure()
ax = fig1.add_subplot(1, 1, 1)

# Plot measured data
ax.plot(current, voltage,
        label="measured data",
        marker="o",
        markersize=8,
        linestyle="none",
        color="blue")

# Create fitted line
yfit = intercept + slope * current

# Plot fit data
ax.plot(current, yfit, 
        color="red",
        label="fit",
        linestyle="dashed")

# Figure options
ax.set_title("Ohm's law analysis on sample")
ax.set_xlabel("I [A]")
ax.set_ylabel("V [V]")
ax.tick_params(axis="both", direction="in")
ax.tick_params(top="on")
ax.tick_params(right="on")
ax.set_xlim(left = 0, right = 6.5E-3)
ax.set_ylim(bottom = 0, top = 2.5)
ax.legend(frameon=False)

# Show plot
plt.show()

# Report values to shell
print(f"intercept = {intercept:.3f} V")
print(f"intercept std. error = {intercept_err:.3f} V")
print(f"slope = {slope:.1f} ohm")
print(f"slope std. error = {slope_err:.1f} ohm")

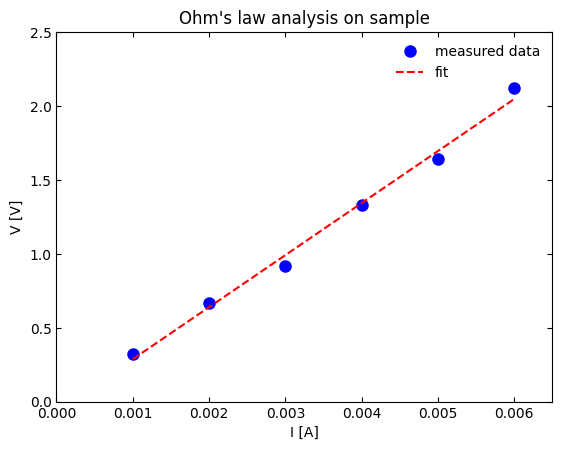
intercept = -0.065 V
intercept std. error = 0.058 V
slope = 352.0 ohm
slope std. error = 14.9 ohm

Mathematically, the R² of a fitting is,

\[ R^2 = 1 - \frac{SS_{res}}{SS_{tot}} \]

where \(SS_{res}\) is called the “residual sum of squares” and \(SS_{tot}\) is called the “total sum of squares”. Let’s first focus on the total sum of squares, \(SS_{tot}\), which is,

\[ SS_{tot} = \sum_{i}^n (y_i - \bar{y})^2 \]

where \(y_i\) is the \(i\)-th dependent variable in a data set of size \(n\) (in our case these are the individual voltage values), and \(\bar{y}\) value is the average of all \(y_i\) values. We can define \(\bar{y}\) as,

\[ \bar{y} = \frac{1}{n} \sum_{i}^n y_i \]

In our example, the voltage values are the \(y_i\) terms. Since these voltages are stored in the array voltage, let’s use the NumPy function numpy.mean() to calculate the average voltage and store it in the variable voltage_mean. This function calculates the average of an entire array or along specified axes. Our array voltage is a one-dimensional array, so we will use the default option to have numpy.mean() calculate the average from all values in the array. The code below demonstrates how to do this.

voltage_mean = np.mean(voltage)
print(f"voltage_mean: {voltage_mean:.3f} V")

voltage_mean: 1.167 V

Now let’s calculate \(SS_{tot}\). The code block below shows how to do this by first creating an intermediate array called deviation_squared that stores the square of the deviation between the voltage values and the average voltage. Then we use another useful NumPy function, numpy.sum(), to sum all the values in deviation_squared (also an array). Similar to numpy.mean(), we can have numpy.sum() sum up along particular axes of an array, but for our needs we need to sum up all values.

deviation_squared = (voltage - voltage_mean)**2
ss_tot = np.sum(deviation_squared)
print(f"ss_tot: {ss_tot:.3f} V^2")

ss_tot: 2.184 V^2

Now let’s define and calculate \(SS_{res}\) (i.e., the other term we need in order to calculate R²). Mathematically, \(SS_{res}\) is defined as,

\[ SS_{res} = \sum_{i}^n(y_i - f_i)^2 \]

where \(f_i\) represents the calculated \(i\)-th dependent variable based on the fitting equation. For our situation, this is our yfit array in the main code block, which we use to create the fit line in the figure.

Hey! Listen!

The deviation between the actual data and model data (i.e., \(y_i - f_i\)) is sometimes referred to as the “residual” or “error”. The phrase “error” can be applied to any situation where you are comparing a value to a reference value. Therefore you may see \(SS_{res}\) equation rewritten in the form,

\[ SS_{res} = \sum_{i}^n(y_i - f_i)^2 = \sum_{i}^n e_i^2 \]

where \(e\) is the “error” between the measured value and the estimated value from a fit.

Let’s go ahead and calculate \(SS_{res}\) for our example,

error_squared = (voltage - yfit)**2
ss_res = np.sum(error_squared)
print(f"ss_res: {ss_res:.3f} V^2")

ss_res: 0.016 V^2

We again use an intermediate variable, this time called error_squared, that stores the deviation between the measured voltages and the modeled voltage values from yfit. We then use the numpy.sum() function to sum up all the values in this array to get \(SS_{res}\).

With these two values, we can now calculate R²:

r_squared = 1 - ss_res / ss_tot
print(f"R squared: {r_squared:.4f}")

R squared: 0.9929

For reference, the code below combines all of these steps together into one single code block.

# Calculate voltage mean
voltage_mean = np.mean(voltage)
print(f"voltage_mean: {voltage_mean:.3f} V")

# Calculate total sum of squares, ss_tot
deviation_squared = (voltage - voltage_mean)**2
ss_tot = np.sum(deviation_squared)
print(f"ss_tot: {ss_tot:.3f} V^2")

# Calculate residual sum of squares, ss_res
error_squared = (voltage - yfit)**2
ss_res = np.sum(error_squared)
print(f"ss_res: {ss_res:.3f} V^2")

# Calculate R squared
r_squared = 1 - ss_res / ss_tot
print(f"R squared: {r_squared:.4f}")

voltage_mean: 1.167 V
ss_tot: 2.184 V^2
ss_res: 0.016 V^2
R squared: 0.9929

3.4. Conclusion#

With a few simple lines of code, we now have a metric that assesses the overall quality of a fit. Since we already are using the NumPy library, we do not need to introduce any additional libraries into our current fitting codes. The setup is generic, and therefore can be implemented to non-linear curve fitting as well. While this lesson goes over the how to calculate R² in Python, this lesson does not cover the meaning of the number or its significance to the quality of a fit. Again, a good review about R² can be found here. The R² metric is one of many ways to determine the overall quality of a fit, with each metric having its own advantages and disadvantages. Hopefully this lesson encourages you to explore and implement fitting metrics for your fitting needs.

3.5. Want to learn more?#

Wikipedia - Coefficient of Determination
NumPy - The numpy.mean() Function
NumPy - The numpy.sum() Function

Data Analysis and Plotting Tips with Python

The R Squared Value of a Fit

Contents