2. Including Uncertainty in Curve Fitting#

2.1. Lesson overview#

In a previous lesson, we demonstrated the basics of curve fitting using the SciPy library. We first showed how to fit a line to set of data and then expanded into non-linear curve fitting. We will now continue our discussion into curve fitting by showing how to incorporate uncertainty values associated with the \(y\)-value of a data point into the least squares regression analysis.

2.2. Topics taught#

Performing least squares analysis using the scipy.optimize.curve_fit() function.
Including measurement uncertainty as weights in scipy.optimize.curve_fit().

2.3. Including uncertainty when fitting data#

To demonstrate how to do this, let’s revisit our non-linear curve fitting example from a previous lesson. We will reuse the majority of the code from this section and update only the necessary lines of code. First, let’s download the raw data file MR_data_with_uncertainty.csv. This file is slightly different from the file we used in the previous example, as it also contains estimates on the uncertainty for both the \(x\)-value (in this case the magnetic field, \(B\)) and the \(y\)-value (the resistance, \(R\)). Even though the data file contains the uncertainty on the \(x\)-values, we will not actually use it in the fitting process, as scipy.optimize.curve_fit() only accounts for the uncertainty on the \(y\)-values.

Let’s re-run our previous code block with some slight adjustments. See the code below, specifically the lines that have the comment NEW FEATURE HERE! nearby. We further discuss the changes below.

# Load libraries
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import curve_fit

# Create function to fit
def parabolaFunc(x, constant, linear, quadratic):
    y = constant + linear * x + quadratic * (x**2)
    return y

# Load data and separate columns (NEW FEATURE HERE!)
data = np.loadtxt("./example_data/MR_data_with_uncertainty.csv", 
                   delimiter = ",", 
                   skiprows = 2)
magnetic_field = data[:,0]
u_magnetic_field = data[:,1]
resistance = data[:,2]
u_resistance = data[:,3]

# Perform the least-squares fitting (NEW FEATURE HERE!)
popt, pcov = curve_fit(parabolaFunc, magnetic_field, resistance, sigma=u_resistance, absolute_sigma=True)

# Extract out the fitted parameters and standard errors
constant = popt[0]
linear = popt[1]
quadratic = popt[2]
constant_err = np.sqrt(pcov[0][0])
linear_err = np.sqrt(pcov[1][1])
quadratic_err = np.sqrt(pcov[2][2])

# Create figure
fig1 = plt.figure()
ax = fig1.add_subplot(1, 1, 1)

# Plot measured data (NEW FEATURE HERE!)
ax.errorbar(magnetic_field, resistance,
            xerr=u_magnetic_field,
            yerr=u_resistance,
            label="measured data",
            marker="d",
            markersize=8,
            linestyle="none",
            color="green",
            capsize=5)

# Create fitted curve
yfit = constant + (linear * magnetic_field) + (quadratic * (magnetic_field**2))

# Plot fit data
ax.plot(magnetic_field, yfit, 
        color="red",
        label="fit",
        linestyle="dashed")

# Figure options
ax.set_title("Magnetoresistance")
ax.set_xlabel("B [T]")
ax.set_ylabel("R [ohm]")
ax.tick_params(axis="both", direction="in")
ax.tick_params(top="on")
ax.tick_params(right="on")
#ax.set_xlim(left=0, right=2.5)
#ax.set_ylim(bottom=0.3525, top=0.3535)
ax.legend(frameon=False)

# Show plot
plt.show()

# Report values to shell
print(f"constant = {constant:.7f} ohm")
print(f"constant std. error = {constant_err:.7f} ohm")
print(f"linear = {linear:.2E} ohm")
print(f"linear std. error = {linear_err:.2E} ohm")
print(f"quadratic = {quadratic:.4E} ohm")
print(f"quadratic std. error = {quadratic_err:.2E} ohm")

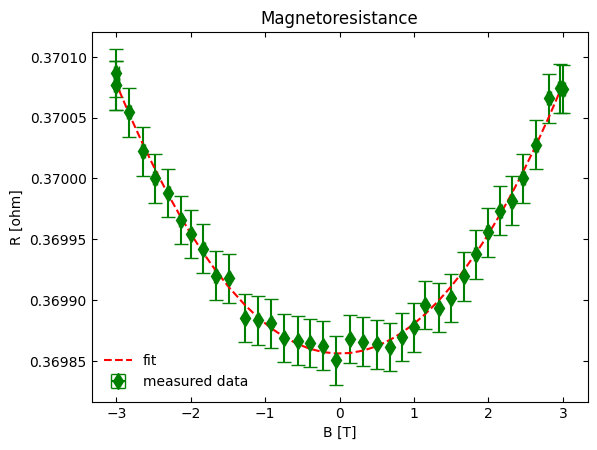
_images/Curve_Fitting_with_Uncertainty_1_0.png

constant = 0.3698562 ohm
constant std. error = 0.0000049 ohm
linear = -2.13E-08 ohm
linear std. error = 1.70E-06 ohm
quadratic = 2.4579E-05 ohm
quadratic std. error = 1.04E-06 ohm

As you can see in the code, this looks very similar to the code used in the non-linear curve fitting example, but with some minor tweaks:

After creating the variable data, we now create separate 1D arrays for the uncertainty on \(B\) and \(R\) called u_magnetic_field and u_resistance, respectively.
The function curve_fit() now contains two additional keyword arguments. The first additional argument is sigma, which represents how much we want to “weigh” the importance of a particular data point to the fit. One common weighting method is called “direct weighting” in which we use the uncertainty of the \(y\)-value as the weighting parameter. In the above example, we do this by setting sigma=u_resistance (i.e., the uncertainty in \(R\)). In this setup, values that have higher uncertainty are weighted more (i.e., prioritized more) in the fit.
The second keyword argument, absolute_sigma=True tells curve_fit() to utilize the actual values provided in sigma in an absolute sense and not in a relative sense. For new users, it is best to set absolute_sigma to True for most situations. Further details on this argument can be found in the online documentation for this function.
When plotting the raw data, we can use the Matplotlib function matplotlib.pyplot.errorbar() to include our uncertainty values as “error bars” to the graph. errorbar() works very similar to plot() and accepts many of the same keyword arguments. The main difference with errorbar() is the addition of the keyword arguments xerr and yerr, which represent the error bar values for the \(x\)- and \(y\)-values, respectively. These are optional arguments, so you do not need to include both arguments when plotting (e.g., sometimes you may want to make a plot with just the \(y\)-value error bars).

And with these changes we now can include the uncertainty of the \(y\)-values to our fits! As you can see in the results, the fitted parameter values and their associated standard errors (i.e., their standard uncertainties) are slightly different compared to when we did not include the uncertainty in the fit.

2.4. Conclusion#

Adding the uncertainty of values to least squares analysis is straightforward with scipy.optimize.curve_fit(). For simple analysis routines, it only requires incorporating two optional keyword arguments to the function call. There are many ways to expand fitting with uncertainty. One common route is to change the weighting of the data in a fit. Our example used a direct weighting scheme, which places more emphasis on data points that have higher uncertainty. The default value for sigma is None, which is equivalent to providing a 1D array of ones. This sets the weight for all values equal to one another, and is the default state in curve.fit(). This weighting scheme was used with the two fitting examples found in the previous basic curve fitting lesson since sigma was not provided in the argument list. There are other ways one can weight the data by modifying what goes into sigma (e.g., instrumental weighting or statistical weighting). These methods often require one to apply a mathematical formula to the uncertainty values in order to weight their importance.

2.5. Want to learn more?#

Wikipedia - Least Squares
Shane Burns - Data Fitting with Error
SciPy Library - The curve_fit() Function
NumPy - Documentation Page
Matplotlib - Home Page

Data Analysis and Plotting Tips with Python

Including Uncertainty in Curve Fitting

Contents